Optimizing Network Structure

Posted 6/14/17

We want to develop an “optimal” network. Here we mean “network” in the scientific sense: Any graph structure from a corporate hierarchy, to a military chain of command, to a computer network apply. What is “optimal” is user-defined - maybe we want to move information as quickly as possible, maybe we want something that works correctly event when many nodes go offline.

Given such a broad problem, the only reasonable solution looks like machine learning. Let’s dive in.

What does the network look like?

Let’s define a network as a DAG, or Directed Acyclic Graph. This is a simplification, as it assumes all communications are one-directional, but this lack of cycles will make the network much easier to reason about.

So the network is a series of nodes, with each lower-level node able to send messages to higher-level nodes (represented as edges).

What does communication look like?

Every message has two costs - one to send and one to receive. Let me justify that in two different scenarios, and we’ll say it generalizes from there.

Human Society:

If I want to communicate an idea I need to express myself clearly. Putting more time and thought in to how I phrase my idea, and providing background knowledge, can make it more likely that I am understood.

If you want to understand the idea I am telling you then you need to pay attention. You can pay close attention and try to follow every word I say, or you can listen/read half-heartedly and hope I summarize at the end.

Computer Network:

I am sending a message over a network with some noise. It could be a wireless network on a saturated frequency, a faulty switch, or just some very long wires with EM interference. I can counteract the noise by adding parity bits or some more complex error correction code. Doing so makes my message longer and requires more CPU time to encode.

Similarly, a receiver needs to decode my message, verify all the checksums, and correct errors. Therefore, transmitting a “better” message costs both bandwidth and CPU time on both ends of the connection.

How do we optimize?

This is already smelling like a machine learning “minimization” or “maximization” problem. All we need now is a continuous scoring function. Something like:

total_score = success_level - cost

From here, we could use a variety of tools like a Neural Network or Genetic Algorithm to maximize the total score by succeeding as much as possible with as little cost as possible.

The “success level” will be defined based on the constraints of the problem, and may be any number of arbitrary measurements:

• How many nodes receive information X propagating from a seed node?
  • How many nodes can get three different pieces of information from different sources and average them?
• How many nodes can be “turned off” while still getting information to the remaining nodes?
• And many others…

Machine Learning Model

A DAG already looks pretty similar to a neural network, so let’s start by using that for our ML model. The model doesn’t quite fit, since neural networks have an “input” and “output” and are typically used for decision making and function approximation. However, the process of adjusting “weights” on each edge to improve the system over time sounds exactly like what we’re trying to do. So this won’t be a typical neural network, but it can use all the same code.

Dynamic Topology

All of the above sounds great for figuring out how much effort to put in to both sides of a communication channel. It even works for optimizing the cost of several edges in a network. But how can it design a new network? As it turns out, pretty easily.

Start with a transitive closure DAG, or a DAG with the maximum possible number of edges:

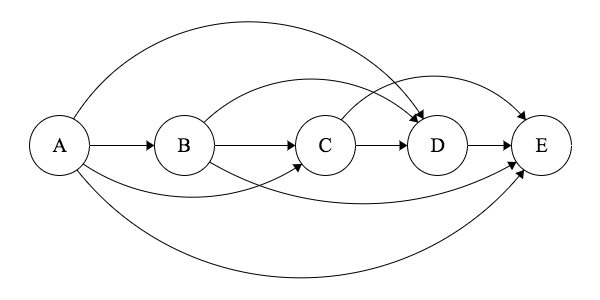
For every edge, if either one side puts no effort in to sending their message, or the other side puts no effort in to receiving a message, then any message that gets sent will be completely lost in noise, and never understood. Therefore, if the receiver cost isn’t high enough on an edge, we can say the edge effectively does not exist.

Coming Soon

Future posts will talk about implementing the system described in this post, applications, and pitfalls.

Attribution

This post is based off of research I am working on at the Santa Fe Institute led by David Wolpert and Justin Grana. Future posts on this subject are related to the same research, even if they do not explicitly contain this attribution.