A Machine Learning Crash Course

Posted 2/28/2026

I am currently teaching a masters level course on network science. We spent one afternoon on a rapid survey of machine learning to introduce students to concepts and tools that can expand their skill sets. I thought it’d make for a good self-contained blog post, so I’ve repurposed the lecture below.

What is Machine Learning?

Machine learning describes a set of statistical techniques for finding predictive patterns in data. Typically, we will have one or more input variables (called features or predictors and denoted X) and one output variable (sometimes called a response variable or a label, denoted y).

Machine learning can be broken into two broad categories, supervised and unsupervised:

• In supervised machine learning we have a series of input data and are trying to find a relationship between multiple features and a known label. For example, “here are labeled photos of cats and dogs, build a machine that can distinguish between the two,” or “we are a life insurance company: based on these spreadsheets of health information and age at death, predict lifespan for future subjects.”

• In unsupervised machine learning we do not have any ground truth labels, and are trying to fit the best pattern possible. For example, clustering, dimensionality reduction, missing value imputation, or outlier detection. Most community detection algorithms from network science fall into this category.

In this post we will primarily be focusing on supervised machine learning. Supervised tasks can be broken into two further categories:

• Classification: produce a categorical label from input data (i.e. “predict whether this is a photo of a cat or a dog”)

• Regression: produce a numeric prediction from input data (i.e. “predict lifespan,” “predict bird beak length”, etc)

Both tasks are closely related, so the algorithms for classification and regression are often quite similar, but model performance is measured a little differently because classification has discrete outputs while regression outputs are continuous.

Linear Regression

Let’s jump in with an example that will motivate more theory. Linear regression: fitting a line to some data. You may have done this with a straight line predicting Y from X since high school or even earlier. We’re doing it again in Python!

We’ll define a “true function” with a nice sinusoidal curve, and draw a few points from that function with noise. Then we’ll try to fit a line to those noisy points to capture the original function. We’ll be making heavy use of Python’s “Scikit-Learn” package, abbreviated sklearn, along with the Numerical Python (numpy) package and MatPlotLib.

#!/usr/bin/env python3
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression

# Adapted from https://scikit-learn.org/stable/auto_examples/model_selection/plot_underfitting_overfitting.html

def true_fun(X):
    return np.cos(1.5 * np.pi * X)

np.random.seed(0)
n_samples = 30

X = np.sort(np.random.rand(n_samples))
X_rotated = X.reshape(-1, 1) # Make this an Nx1 array instead of 1xN
y = true_fun(X) + np.random.randn(n_samples) * 0.1 # True function with a little noise

reg = LinearRegression().fit(X_rotated, y)
score = reg.score(X_rotated, y)

# Use one hundred points from 0..1 to plot our model and the original function
X_test = np.linspace(0, 1, 100)
X_test_rotated = X_test.reshape(-1,1)
plt.figure(figsize=(6,4), dpi=120)
plt.plot(X_test, reg.predict(X_test_rotated), label="Model")
plt.plot(X_test, true_fun(X_test), label="True Function")
plt.scatter(X, y, edgecolor="b", s=20, label="Samples")
plt.xlabel("x")
plt.ylabel("y")
plt.xlim((0,1))
plt.ylim((-2,2))
plt.title("$R^2$ of %.3f" % score)
plt.legend(loc="best")
plt.show()

Here we’ve fit a straight line to data points drawn from a curve. The line is not an especially good match. What if instead of providing x as an input, we provide x, x^2, x^3, and so on up to an arbitrary degree? This should let us fit a curve instead of a straight line:

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

degrees = [2, 4, 15]

fig, axs = plt.subplots(1, 3, figsize=(14,5), sharex=True, sharey=True)
for i,degree in enumerate(degrees):
    ax = axs[i]
    expanded_features = PolynomialFeatures(degree).fit_transform(X_rotated)
    reg = LinearRegression().fit(expanded_features, y)
    score = reg.score(expanded_features, y)

    X_test = np.linspace(0, 1, 100)
    X_test_rotated = PolynomialFeatures(degree).fit_transform(X_test.reshape(-1,1))
    ax.plot(X_test, reg.predict(X_test_rotated), label="Model")
    ax.plot(X_test, true_fun(X_test), label="True Function")
    ax.scatter(X, y, edgecolor="b", s=20, label="Samples")
    ax.set_xlabel("x")
    ax.set_ylabel("y")
    plt.xlim((0,1))
    plt.ylim((-2,2))
    ax.legend(loc="best")
    ax.set_title("Degree %d\n$R^2$ = %.3f" % (degree,score))
plt.show()

What’s going on?

With a polynomial of degree 1, we’re fitting y = mx + b, where linear regression is tuning two variables to our data: m and b. In order to fit our line to data we need some metric of how good a fit we have, commonly called a loss function or error function. Common choices are mean-squared error (MSE), and mean-absolute error (MAE). Above we’re using MSE, where error = sum(true_y - predicted_y)**2. This minimimizes the importance of small errors, and magnifies the importance of large errors. We adjust m and b experimentally until we find the lowest possible error score.

Note that rather than displaying MSE directly, we present it as an R^2 score, which is defined as 1 - u/v where u is MSE and v is sum (true_y - mean_y)**2. This ranges from (-infinity,1] where 1 is a perfect score and 0 is “guesses the mean answer for every input.”

When we increase the degree of the polynomial to 4, we are now fitting a separate “feature weight” or importance score to each input:

This is a generalization of our original y = mx + b with a separate weight for each input feature. In this case our features are x, x^2, and so on, but they could be independent variables. Now there are many more knobs to tune, but we still have a linear combination of input variables to fit a curve. With a degree of four we can make a curve very close to the original input function, greatly improving our model’s predictive power.

So what went wrong in the third figure? When we increase the model degree to 15 we now have an enormous number of knobs to tune. By carefully adjusting the parameters we can tweak our curve to pass through almost every point directly, increasing our score even further! But our curve looks nothing like the original function. We have overfit to the training data, losing sight of the pattern we’re trying to capture in favor of getting the highest possible score.

A significant challenge in machine learning is optimizing your model to get the highest predictive power possible without overfitting. We have many tools at our disposal to detect and inhibit overfitting. We will cover some of them later. (If you are shaking your computer screen screaming about train/test splits, we’re building up to it!)

Logistic Regression

For now let’s turn our focus towards a classification problem instead of a regression problem. Logistic regression fits a line to input variables much like linear regression. However, we’re going to fit a logistic sigmoid function with the form:

This produces an S-shaped curve where the y-value ranges from 0 to 1. For binary classification (distinguishing between two categories) we can treat 0 as the first category, 1 as the second category, and any value in-between as a degree of uncertainty:

We can interpret this curve as telling us “the probability that the data point is in category 1 is p(x), and the probability that the data point is in category 2 is 1 - p(x).” Therefore, probabilities sum to 1, because there is a 100% chance of the data point belonging to some category.

If we have more than two categories we must use multinomial logistic regression. (Organ music plays) Here we have multiple S-shaped curves, and the probabilities across all curves must sum to one. For a given category i this can be expressed as:

This is basically just a normalized version of ordinary logistic regression. Now let’s apply this theory to the Iris dataset. This is a classification dataset containing three kinds of irisis (Setosa, Versicolour, and Virginica). For each flower, we’ve recorded the sepal length and width, and the petal length and width, giving us four numeric features in centimeters and 150 example flowers.

from sklearn.datasets import load_iris
X, y = load_iris(return_X_y=True)
print("Five example flowers:")
print(X[:5,:])
print("The categorical labels for all flowers:")
print(y)

Five example flowers:
[[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 [4.6 3.1 1.5 0.2]
 [5.  3.6 1.4 0.2]]
The categorical labels for all flowers:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

Let’s fit logistic regression to the data, and then ask it to classify the first two flowers:

from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(random_state=0,max_iter=1000).fit(X,y)
print("Predicted labels for first two flowers:")
print(clf.predict(X[:2, :]))
print("Probabilities for each class for first two flowers:")
print(clf.predict_proba(X[:2, :]))
print("Accuracy across all flowers:")
print(clf.score(X, y))

Predicted labels for first two flowers:
[0 0]
Probabilities for each class for first two flowers:
[[9.81567923e-01 1.84320627e-02 1.44928093e-08]
 [9.71336447e-01 2.86635225e-02 3.01765481e-08]]
Accuracy across all flowers:
0.9733333333333334

Both of the first flowers are category zero (Iris Setosa), and we can see that the model was 98 and 97% confident of both classifications, respectively. It predicted 2-3% odds that the flowers might be Iris-Versicolour, but effectively no chance of Iris-Virginica. In general, the model classifies 97% of all flowers correctly.

What is a ‘Good’ classifier?

A perfect classification model labels every data point correctly. But what if our model is only pretty good? How do we describe how good it is? We have a great many metrics to choose from. Common choices include accuracy, recall, false positive rate, precision, F1-score, ROC-AUC, and MCC. Here’s a description of each, where TP, TN, FP, and FN represent true positives and negatives, and false positives and negatives, respectfully:

• Accuracy: correct classifications / total classifications, or (TP + TN)/(TP + TN + FP + FN)

• Recall: correct positives / all positives, or TP / (TP + FN), “how many of the positives did we find?”

• False Positive Rate (FPR): incorrect negatives / all actual negatives, or FP / (FP + TN)

• Precision: correct positives / everything marked as positive, or TP / (TP + FP), “when we marked something as positive, how often were we right?”

• F1 score (balanced F-score): (2 * TP) / (2 * TP + FP + FN), harmonic mean of precision and recall

• ROC-AUC (Area under the curve from a Receiver Operating Characteristics curve)

• Matthews correlation coefficient (MCC): (TP * TN - FP * FN) / sqrt((TP + FP)(TP + FN)(TN + FP)(TN + FN))

Why so many? Because a ‘good’ model is context-dependent. In a medical test, maybe we care about identifying sick people for treatment, and accidentally treating a few healthy people is preferable to missing a few sick people. For your spam filter, maybe you’ll be a little annoyed if an occasional spam email lands in your inbox, but you’ll be very annoyed if an important email goes into your spam folder unnoticed.

In addition to the subjective importance of false positives and false negatives, some of the scores above suffer under class imbalance. In the iris dataset we have three classes of irisis, and they are equally represented (50 each). But what if 80% of the flowers were Iris Virginica? You’ll now get very skewed values, where a high accuracy score may not mean much - if you always guess Iris Virginica you’ll get 80% accuracy! With imbalanced datasets we typically prefer the F1 score or MCC, which are more robust but less intuitive.

Decision Trees

Linear and logistic regression are both line-fitting algorithms. We will now introduce a different family of machine-learning approaches: decision trees. This is set of algorithms that sub-divides your dataset into small regions, ultimately producing a flowchart to yield predictions. Decision trees are referred to as classification trees when used for classification, and regression trees when used for regression, but the techniques are almost identical.

Let’s begin with a dataset of blue squares and orange circles (our categorical labels), each of which have an X and Y value.

We now try to place a vertical line that best separates the squares and circles, and a horizontal line that best separates the classes. We’ll keep whichever line works best.

The right partition contains only blue squares, so we’re done processing it. The left partition can be further sub-divided, so we repeat the process recursively. First we add another vertical line:

Then we add a horizontal line:

Now that the full data set is divided into partitions, the model uses these partitions for prediction. For any given X and Y values, identify the partition containing that value, and return the mode of the training data points within the partition. This can be generalized from two dimensions to an arbitrary number (although it becomes far more challenging to visualize, of course): we just look for a line along each axis that creates a partition where the variance within partitions is low, and the variance across partitions is high.

We can define several stopping conditions for building our tree. Maybe we stop once a partition has below three data points in it. Maybe we stop at a maximum depth of four. Maybe we stop once most or all of the points in a partition have the same label.

Here’s the above decision tree implemented with sklearn:

from sklearn.tree import DecisionTreeClassifier, plot_tree
X = [
    [2, 4],
    [3, 5],
    [3, 2],
    [1, 1],
    [5, 1],
    [6, 3],
    [6, 4],
    [7, 2]
    ]
y = [1, 0, 0, 0, 0, 1, 1, 1]

clf = DecisionTreeClassifier()
clf = clf.fit(X, y)
plot_tree(clf, feature_names=["X", "Y"], class_names=["Red", "Blue"], filled=True, rounded=True, impurity=False, fontsize=10)
plt.show()

The plot_tree function can export our decision tree as a flowchart:

This is magnificent! If neural networks are a black box where it’s difficult to understand how the model comes to a conclusion, decision trees are the inverse, where it is transparently clear how decisions are made. My mantra: if your machine learning task is simple enough to solve with a flowchart, then you should always solve it with a flowchart. You’d be surprised how many times a seemingly-complicated machine learning problem can be solved with a few if-statements - sometimes heuristics work great!

Regression Trees

When applying decision trees to regression problems instead of classification problems, the algorithm is almost identical. As with classification trees, regression trees divide data points into partitions that maximize variance between the partitions, and minimize variance within the partitions. However, the regression tree predicts values using the mean of the points within a partition, while a classification tree uses the mode. We also measure performance differently for classification and regression trees - for classification we’ll use accuracy or recall or any of the metrics defined above, while regression will use a loss function like “mean squared error” as in the linear regression example.

Classifying Irises using Trees

For a more involved example, let’s throw decision trees at the Iris dataset. We’ll limit trees to depth of 2, 3, and 5, report the accuracy score of each, and then plot the depth-3 tree:

from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.datasets import load_iris
X, y = load_iris(return_X_y=True)

trees = []

for max_depth in [2, 3, 5]:
    clf = DecisionTreeClassifier(
        max_depth=max_depth,
        min_samples_split=2,
        min_samples_leaf=1,
        min_impurity_decrease=0.005,
        max_leaf_nodes=None
    ).fit(X, y)
    score = clf.score(X, y)
    print("Max-depth %d has an accuracy of %.3f" % (max_depth,score))
    trees.append(clf)

feature_names = ["Sepal Length", "Sepal Width", "Petal Length", "Petal Width"]
class_names = ["Iris-Setosa", "Iris-Versicolour", "Iris-Virginica"]
plt.figure(figsize=(14, 5), dpi=120)
plot_tree(trees[1], feature_names=feature_names, class_names=class_names, filled=True, rounded=True, impurity=False, fontsize=10)
plt.show()

Max-depth 2 has an accuracy of 0.960
Max-depth 3 has an accuracy of 0.973
Max-depth 5 has an accuracy of 0.993

Summarizing the tree: if the Iris has narrow petals, it’s Iris-Setosa. Otherwise, if the petals are very wide, it’s Iris-Virginica. In the less clear intermediate region, if the petals are long it’s probably Iris-Virginica, and if the petals are shorter it’s almost certainly Iris-Versicolour. Logistic regression couldn’t explain its decision-making process this way!

Notice that I’ve added an extra boundary condition: min_impurity_decrease. This restricts the tree so that we don’t divide partitions unless the new cut significantly improves variance scores. This prevents the tree from sub-dividing the rightmost Iris-Virginica partition to try and separate out that single Iris-Versicolour sample in the bin.

Fitting a Regression Tree to a Curve

Let’s return to our linear regression problem, but this time face it with regression trees:

from sklearn.tree import DecisionTreeRegressor, plot_tree

def true_fun(X):
    return np.cos(1.5 * np.pi * X)

np.random.seed(0)
n_samples = 30

X = np.sort(np.random.rand(n_samples))
X_rotated = X.reshape(-1, 1) # Make this an Nx1 array instead of 1xN
y = true_fun(X) + np.random.randn(n_samples) * 0.1 # True function with a little noise

X_test = np.linspace(0, 1, 1000)
X_test_rotated = X_test.reshape(-1,1)

plt.clf()
trees = []
fig, axs = plt.subplots(1, 3, figsize=(14,5), sharex=True, sharey=True)
for i,max_depth in enumerate([2, 3, 7]):
    reg = DecisionTreeRegressor(
        max_depth=max_depth,
        min_samples_split=2,
        min_samples_leaf=1,
        max_leaf_nodes=None
    ).fit(X_rotated, y)
    trees.append(reg)

    score = reg.score(X_rotated, y)

    ax = axs[i]
    ax.plot(X_test, reg.predict(X_test_rotated), label="Model")
    ax.plot(X_test, true_fun(X_test), label="True Function")
    ax.scatter(X, y, edgecolor="b", s=20, label="Samples")
    ax.set_xlabel("x")
    ax.set_ylabel("y")
    plt.xlim((0,1))
    plt.ylim((-2,2))
    ax.legend(loc="best")
    ax.set_title("Max Depth %d\n$R^2$ = %.3f" % (max_depth,score))
    
plt.show()
plt.figure(figsize=(14, 5), dpi=120)
plot_tree(trees[1], feature_names=["X"], filled=True, rounded=True, impurity=False, fontsize=10)
plt.show()

This lets us plot example performance with several regression trees of different depths:

First, this is clearly much blockier than linear regression, and does not neatly capture the original function. Nevertheless, we get a decent R^2 score, especially as we increase the tree depth and begin mercilessly overfitting to training data.

Let’s examine the depth three tree in more detail:

As we can see, the tree simply bins the training data points and predicts one of eight values. A clumsy heuristic, but it’s performed well enough so far. Note that this strategy will not work if we apply our decision tree to any X values not well represented in the training data. With linear regression, we can fit our degree 4 polynomial to the original function and effectively predict what the function will likely do for an X value of 1.2 - but our regression tree will simply return the value of its highest bin and guess -0.2 for all X values above 0.935! Terrible!

Limitations of Trees

Trees are wonderful for their simplicity and explainability, their ability to easily work with categorical features, and their robustness to features of different scales. Truly a wonderful technique. Unfortunately, they do have a number of downsides:

• They are prone to overfitting, and must be carefully constrained

• They are bad at extrapolation: linear regression can predict a y-value based on a trajectory from a known data point, while decision trees can only bin y-values to the closest data point in their training set

• They can produce poor trees for heavily biased datasets

For the above reasons decision trees are rarely used on their own in production applications of machine learning. They are however, often used as components of more sophisticated algorithms.

Random Forests

What do we do when trees overfit? Add more trees!!

Decision trees are prone to overfitting. One solution to this problem is to create multiple decision trees, each fit on a subset of the available features and training data. Each tree may overfit to the training data, but they’ll overfit in different ways. We can average the predictions from each tree and get a superior aggregate result. We call this collection of random-feature trees a Random Forest. In general, models that average the results of other models are called ensemble models.

Random forests perform much better than trees. While they typically don’t quite match more advanced approaches like deep neural networks or generative AI, they are simple and computationally much cheaper. For this reason they are often included as a baseline when measuring the performance of more advanced models, and random forests are still often deployed for their better performance / cost ratio.

Trees and forests also have one last advantage: they can easily report how useful each feature was in prediction. We’ll demonstrate this by applying Random Forests to another classic dataset: predicting who survived the sinking of the Titanic. In this problem we have a number of input features - some categorical, such as sex or passenger class, some numeric, like age or ticket cost - and we are fitting a binary classifier to answer “is a given passenger likely to survive?”

For now, please gloss over the Ordinal Encoding and Imputation lines; we will return to them later. Suffice to say they’re cleaning up a messy dataset and preparing the inputs in a format better-suited to machine learning.

# Adapted from https://scikit-learn.org/stable/auto_examples/inspection/plot_permutation_importance.html

from sklearn.datasets import fetch_openml
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OrdinalEncoder
from sklearn.impute import SimpleImputer
from sklearn.ensemble import RandomForestClassifier

X, y = fetch_openml("titanic", version=1, as_frame=True, return_X_y=True)

categorical_columns = ["pclass", "sex", "embarked"]
numerical_columns = ["age", "sibsp", "parch", "fare"]
# Reorder columns and drop irrelevant data
X = X[categorical_columns + numerical_columns]

categorical_encoder = OrdinalEncoder(handle_unknown="use_encoded_value", unknown_value=-1, encoded_missing_value=-1)
numerical_pipe = SimpleImputer(strategy="mean")
preprocessing = ColumnTransformer(
    [
        ("cat", categorical_encoder, categorical_columns),
        ("num", numerical_pipe, numerical_columns),
    ],
    verbose_feature_names_out=False,
)

X = preprocessing.fit_transform(X)

rf = RandomForestClassifier(n_estimators=100, random_state=0)
rf.fit(X, y)

feature_names = categorical_columns + numerical_columns
mdi_importances = pd.Series(rf[-1].feature_importances_, index=feature_names).sort_values(ascending=True)
ax = mdi_importances.plot.barh()
ax.set_title("Random Forest Feature Importances\nBy Mean Decrease in Impurity")
plt.show()

We can’t get a nice flowchart out of our forest, because the forest is averaging one hundred decision trees, each of which have a handful of features to work with. However, the above plot tells us that sex and age were the most helpful features for determining survivability, followed by fare, followed distantly by everything else. In other words, “women and children first, and the lifeboats were on the upper decks near the higher-paying travelers.”

Note that the above features are not necessarily independent. We can imagine a scenario where most of the women and children on the boat were higher-paying travelers, while the lower decks were filled with male immigrants seeking work. In this case, there may be some overlapping information between sex, age, and fare, but we can fit to the decision problem nevertheless. Likewise, we might expect that ticket fare and passenger class correlate, but ticket price had a higher resolution and provided a better signal than passenger class alone, and so was favored in any tree with access to both.

Train / Test Splits

So far we have trained our models on all of our example data points, and then measured the model’s performance by how well it predicts those same data points. This is a recipe for disastrous overfitting. The model can easily memorize all inputs and achieve perfect accuracy that’s useless in the real world! We’ve seen examples of this already with degree-15 linear regression and depth-7 regression trees.

Instead, we typically want to train on some data points, and test performance on a second set of points. How many? It’s a tradeoff: more training data will improve our model, but we want to withhold enough data for testing to be confident about our model performance.

One unprincipled and clumsy rule of thumb is the 80-20 split: use 80% of our data for training, 20% for testing. Let’s give it a shot! Starting with the line-fitting problem once again:

from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.preprocessing import PolynomialFeatures
from sklearn.model_selection import train_test_split

def true_fun(X):
    return np.cos(1.5 * np.pi * X)

np.random.seed(0)
n_samples = 40
linear_regression_polynomial = 2
tree_depth = 7

X = np.sort(np.random.rand(n_samples))
y = true_fun(X) + np.random.randn(n_samples) * 0.1 # True function with a little noise
X_rotated = X.reshape(-1, 1)

# 80/20 train/test split
X_train, X_test, y_train, y_test = train_test_split(X_rotated, y, train_size=0.8)

# Expand train and test X for linear regression
train_expanded_features = PolynomialFeatures(linear_regression_polynomial).fit_transform(X_train)
test_expanded_features = PolynomialFeatures(linear_regression_polynomial).fit_transform(X_test)

# Fit both models
lreg = LinearRegression().fit(train_expanded_features, y_train)
treg = DecisionTreeRegressor(max_depth=tree_depth).fit(X_train, y_train)

# Get R^2 for train and test sets
lin_train_score = lreg.score(train_expanded_features, y_train)
lin_test_score = lreg.score(test_expanded_features, y_test)
treg_train_score = treg.score(X_train, y_train)
treg_test_score = treg.score(X_test, y_test)

X_plot = np.linspace(0, 1, 1000)
X_plot_rotated = X_plot.reshape(-1,1)
X_plot_expanded = PolynomialFeatures(linear_regression_polynomial).fit_transform(X_plot_rotated)

fig, axs = plt.subplots(1, 2, figsize=(14,5), sharex=True, sharey=True)
axs[0].plot(X_plot, lreg.predict(X_plot_expanded), label="Linear Regression")
axs[1].plot(X_plot, treg.predict(X_plot_rotated), label="Regression Tree")
for i in [0,1]:
    axs[i].plot(X_plot, true_fun(X_plot), label="True Function")
    axs[i].scatter(X_train.reshape(-1, 1), y_train, edgecolor="b", s=20, label="Training Samples")
    axs[i].scatter(X_test.reshape(-1, 1), y_test, edgecolor="r", s=20, label="Testing Samples")
    axs[i].set_xlabel("X")
    axs[i].set_ylabel("Y")
    axs[i].legend(loc="best")
axs[0].set_title("Linear Regression train $R^2$ %.3f Test $R^2$ %.3f" % (lin_train_score, lin_test_score))
axs[1].set_title("Regression Tree train $R^2$ %.3f Test $R^2$ %.3f" % (treg_train_score, treg_test_score))
plt.xlim((0,1))
plt.ylim((-2,2))
plt.show()

This is a good start: already we can see how linear regression did okay at capturing the training data, but didn’t match the original pattern well enough to do so well on our hold-out testing data. Meanwhile, the regression tree overfit to the training data by a great deal and performs a little worse on the test data.

However, the 80-20 rule can easily get us in trouble. The big concern is class imbalance. For a regression task: what if most of the training data is in the lower-right portion of the plot, and most of the test data is in the upper left? For a classification task: what if the training data consists mostly of Iris-Setosa and Iris-Versicolour, but the test data consists mostly of Iris-Virginica? This can be especially challenging if one class is rare to begin with, and absent or nearly absent in the training data.

There are a variety of solutions to this problem. Here are two:

Stratified Sampling

Perform a stratified split. Still an 80-20 (or any other sized) shuffle, but we now maintain approximately the same ratio of classes in train and test data.

X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)

We may occasionally want to stratify on features instead of (or in addition to) labels. For example, if we’re predicting a disease based on medical records and there are very few patients with high blood pressure in our records, you may want to make sure there are a few in both the training and testing sets.

Cross-Validation

Perform cross validation. Here we perform an 80-20 (or any other) split many times, and report average model performance. This can be especially useful in regression tasks where there aren’t clear categorical classes, but we want to be sure the model didn’t receive an “easy” or “hard” training set.

from sklearn.model_selection import cross_validate
# Here 'reg' is any regression model. You can also use a classifier if you
# switch from measuring R^2 to accuracy or another categorical score
cv_results = cross_validate(reg, X, y, cv=3)
cv_results['test_score'] # Returns an array of each R^2

The variance of test scores can tell us how stable our model is, and whether randomly shuffling the input data leads to wildly divergent results. If the model isn’t stable, then we need to take a hard look at our dataset - we probably need to perform stratification and just haven’t identified the appropriate features or bins yet.

The Model Complexity Tradeoff

Generally, simple models are less flexible and require that you specify more of the solution upfront. For example, linear regression fit a polynomial, but only when we specified the degree of the polynomial as a hyperparameter, or a setting chosen by the scientist rather than fit to data. However, simple models are fast to train, require comparatively little data, and are easier to explain. This makes them preferable for causal inference, when we are trying to understand a relationship and what causes a pattern to emerge.

More sophisticated models are more flexible, and can discover patterns with less of the structure pre-defined. However, these models require much more training data, are slow to train, and are much more difficult to explain. They can often get higher performance in classification and regression tasks, but are less useful for causal inference. These are more common in industry applications where making the tool work better is prioritized over answering scientific questions.

A very hand-wavey scale of model complexity might be:

Feature Preparation

We’ve covered all of the models we’ll discuss in this post, but there are a number of tasks surrounding machine learning that I want to cover.

Normalization

Some models only work well if all input features have a similar range. For example, in the California Housing dataset we are predicting housing prices - some features have small values (AveRooms), while some features have much larger values (median income for families in the region).

You can use normalization tools like MinMaxScaling to rescale a feature to [0,1], [-1,1], or whatever other range is appropriate. This can ensure that models don’t implicitly treat larger features as more important, or make them more sensitive to small changes in some features over others.

Sometimes it is appropriate to bin features to decrease resolution - especially when combining multiple datasets with different resolutions. For example, if you are predicting penguin species by beak length, and penguin data from one study measures the beak length in millimeters, while another categorizes “short,” “medium,” “long,” you’ll need to convert the numeric data to the lower resolution to meaningfully combine the data.

Categorical Encoding

Most machine learning models cannot directly handle categorical features. To convert categorical features to numeric consider both ordinalization and one-hot encoding.

Ordinalization simply assigns an index to every discrete value for a feature. Here we define two features: a binary gender (boo!), and a numeric category:

from sklearn.preprocessing import OrdinalEncoder, OneHotEncoder

ordEnc = OrdinalEncoder()

X = [['Male', 1], ['Female', 3], ['Female', 2]]

ordEnc.fit(X)
print(ordEnc.categories_)
print(ordEnc.transform([['Female', 3], ['Male', 1]]))
print(ordEnc.inverse_transform([[1, 0], [0, 1]]))

[array(['Female', 'Male'], dtype=object), array([1, 2, 3], dtype=object)]
[[0. 2.]
 [1. 0.]]
[['Male' 1]
 ['Female' 2]]

Ordinalization converts the first column to [0,1], and the second column to [0,1,2], after we fit to some example features to learn the appropriate values. We can transform features into ordinal form, or inverse_transform back to original string and number values.

Why might this be a bad idea? What assumptions does a numeric feature have?

Consider that this assumes one categorical value is numerically greater than another, and we assert that categorical values can be ordered on a number line. What kinds of undesired patterns might an ML model latch onto given these implications? Logistic regression will try to fit a curve to these points, even if that doesn’t make sense.

One Hot encoding instead expands one feature into an array of boolean features:

oneEnc = OneHotEncoder()

oneEnc.fit(X)
print(oneEnc.categories_)
print(oneEnc.transform([['Female', 3], ['Male', 1]]).toarray())
print(oneEnc.inverse_transform([[0, 1, 1, 0, 0], [1, 0, 0, 0, 1]]))

[array(['Female', 'Male'], dtype=object), array([1, 2, 3], dtype=object)]
[[1. 0. 0. 0. 1.]
 [0. 1. 1. 0. 0.]]
[['Male' 1]
 ['Female' 3]]

Now instead of a single “gender” feature we have a “male” feature and a “female” feature, one of which will always be 1, or “hot”, while the other will be zero. Likewise, we convert the second numeric column into three features, representing whether the data takes on category 1, 2, or 3.

This has a few implications. First, we’ll have a lot more features, and thus more feature weights, complicating training. We’ll also have separate feature weights for each categorical value - so we’ll no longer have a feature importance for “gender”, but a feature importance for “male” and a separate importance for “female.” Depending on the setting this might be irrelevant, or might make it harder to identify what features are most significant to the model.

Missing Data

In an ideal world, your input features are a nice and complete spreadsheet. In reality, your spreadsheet will often have holes in it. Maybe a sensor failed and returned no reading. Maybe we’re transcribing written records, and a piece of handwriting was indecipherable. Maybe we have a value, but it’s so far out of range that we’re sure it’s incorrect.

A machine learning model requires complete data. Linear regression can’t fit to X = undefined. What do we do about these holes?

In an undergraduate machine learning course we might instruct students to simply drop any row containing a null value. Unfortunately, this often throws away a lot of training data. Say we have twenty features for medical records, but we got a bad blood sugar reading. Do we discard all 19 valid records for the patient because a single data point is invalid? If enough rows are missing a value, this could significantly shrink the training data set.

We can do better. We can use imputation.

We will fill the holes in our data with an educated guess. This is ideologically uncomfortable: we’re training our ML model on made up data! Surely this will make the model worse! But if we can recover 19 real data points for the cost of one fake data point, maybe this is a net positive for the model, especially if our fake data point is close to the correct value.

So what’s an appropriate educated guess? Sometimes the mean. Missing blood sugar? Fill in a mean blood sugar score. Missing heart rate? Mean resting heart rate. It probably won’t be orders of magnitude off - certainly better than filling in 0.

from sklearn.impute import SimpleImputer

imp = SimpleImputer(missing_values=np.nan, strategy="mean")
imp.fit([
    [1, 2], 
    [np.nan, 3], 
    [7, 6]])

X = [
    [np.nan, 2], 
    [6, np.nan], 
    [7, 6]]
print(imp.transform(X))

[[4.         2.        ]
 [6.         3.66666667]
 [7.         6.        ]]

Here we’ve fit to some data to learn the mean (4 for the first column, skipping over the hole, just over three and a half for the second column), and then transformed a set of features to fill in the holes with the mean.

But often the mean is not a good choice. For time series data we can often use the previous data point, or an average of the previous and next, or the average of a rolling window. For example, say we’re predicting weather, and gathering features about temperature and humidity and wind speed and a dozen other factors at hourly intervals. We’re missing a temperature reading for one row. Appropriate educated guesses might include an average of the temperature from the previous and next hour, or perhaps “the temperature at this time yesterday.” Both are better than the mean temperature for the day, week, or year.

Sometimes we don’t want to impute using a single feature, but by using multiple features. For example, instead of filling in “mean resting heart rate,” maybe you can do better with “mean resting heart rate for patients of a similar age, weight, blood pressure, etc.” One strategy here is to use K-Nearest-Neighbors. Simply find the closest few neighboring data points that aren’t missing any features, and take the mean of those.

from sklearn.impute import KNNImputer

imp = KNNImputer()
imp.fit([
    [1, 2], 
    [np.nan, 3], 
    [7, 6]])

X = [
    [np.nan, 2], 
    [6, np.nan], 
    [7, 6]]
print(imp.transform(X))

[[4. 2.]
 [6. 4.]
 [7. 6.]]

By default we perform a weighted mean - find the closest few neighbors, average their scores for the missing feature, but weigh closer neighbors more highly than distant neighbors.

We can get much fancier than k-Nearest-Neighbors, and train an entire model to perform imputation for us. Random Forest is a popular choice. IterativeImputer can utilize any underlying regression model for imputation.

One Hazard!

Be sure that your missing values do not follow a pattern of their own. If you are missing resting heart rate values for a handful of patients at random, mean imputation may be an effective reconstruction strategy. If you are missing resting heart rate values for patients with high blood sugar, then using unifeature imputation like a column mean is a bad strategy, and a multifeature imputation technique like kNN will serve you much better. Likewise, if null values correlate, for example you are often missing heart rate and blood sugar readings, then reconstruction will be much more difficult and it may make sense to drop those rows. Imputation is an imperfect science of educated guesses, and we must be careful that our fake data does not do more damage than our recovered rows help.

De-correlation through dimensionality reduction

Say you have many features. Perhaps too many to train on. Or, you have several features that closely correlate with one another. This can be a big problem for some models like Random Forests: we want to make sub-trees that have access to different features, but if many features correlate then most or all trees will have access to the same underlying pattern and so overfit similarly, undermining the forest.

We can address these problems by reducing our feature set using dimensionality reduction. There are many tools for this, including PCA, LDA, t-SNE, and UMAP.

Let’s make an example using our Iris dataset again, where we’ll reduce our starting four features to two features using Principal Component Analysis:

from sklearn.decomposition import PCA

X, y = load_iris(return_X_y=True)

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
(pca1_explained, pca2_explained) = pca.explained_variance_ratio_ * 100

plt.figure(figsize=(8, 6))
colors = ['orange', 'green', 'blue']
shapes = ["o", "s", "^"]
class_names = ["Iris-Setosa", "Iris-Versicolour", "Iris-Virginica"]

for i in [0, 1, 2]:
    X1s = X_pca[y == i, 0]
    X2s = X_pca[y == i, 1]
    class_name = class_names[i]
    color = colors[i]
    shape = shapes[i]
    plt.scatter(X1s, X2s, alpha=0.8, color=color, marker=shape, label=class_name)

plt.legend(loc='best') 
plt.title('PCA of Iris dataset')
plt.xlabel('Principal Component 1 (Explains %d%% of variance)' % pca1_explained)
plt.ylabel('Principal Component 2 (Explains %d%% of variance)' % pca2_explained)
plt.show()

These two axes are linear combinations of our original four features, chosen so that they explain as much of the variance of the original data as possible. The first principal component explains 92% of the variance of the original flower dataset, while the second component picks up another 5%. This means we’ve lost a little information - we did go from four dimensions to two after all - but we can still capture 97% or so of the original variation. This tracks with our understanding of the data; remember that our decision tree only used the petal width and length to distinguish flowers, and didn’t use the sepal dimensions at all, so perhaps two axes are enough to sufficiently describe our data. Let’s train a classifier on our principal components to confirm:

clf = DecisionTreeClassifier(
    max_depth=2,
    min_samples_split=2,
    min_samples_leaf=1,
    min_impurity_decrease=0.008,
    max_leaf_nodes=None
).fit(X_pca, y)
score = clf.score(X_pca, y)

feature_names = ["PCA 1", "PCA 2"]
plt.figure(figsize=(14, 5), dpi=120)
plot_tree(clf, feature_names=feature_names, class_names=class_names, filled=True, rounded=True, impurity=False, fontsize=10)
plt.title("Depth-2 Decision Tree has an accuracy score of %.3f" % score)
plt.show()

The classification tree yields two if-statements, both based on the first principal component, and correctly classifies almost 95% of the Irises. This is marginally worse than the original tree, which scored 96% with a depth of two. We have also lost most of our explainability: sure, the tree can score quite well with two if-statements, but we no longer have an intuitive flowchart utilizing petal width and length. Nevertheless, this demonstrates how we can shrink many-featured datasets to fewer features, eliminate duplicate or closely correlated features, and train an effective machine learning model on the results using fewer feature weights, and therefore less training time. There are many advantages to this technique.

Conclusion

In this post we’ve introduced about four models: linear regression, logistic regression, decision trees (of classification and regression variety), and random forests (of either variety of tree). These are foundational models, chosen for their simplicity rather than state-of-the-art performance, and we’ve used them to explore training and testing, and a variety of feature preparation techniques. This overview of supervised machine learning is intended to provide a survey of concepts in the field, and better equip you to learn more machine learning techniques on your own.

Bayesian Network Science

Posted 1/26/2026

I am currently teaching masters students to perform statistical network analysis, especially predicting the structure of a network from observational data, calibrating network models to real-world data, and rejecting hypotheses about the structure of networks. This post repurposes my recent lecture for a more general audience. It is more math-heavy than most of my posts, and involves some statistics and light differential equations, and assumes some familiarity with graph theory or network science.

What is Bayesian Statistics?

Statistical techniques can be broadly put in two categories:

• Frequentist Statistics uses evidence to estimate a point value. Probabilities are interpreted as long run frequencies.

• Bayesian Statistics uses evidence and a set of prior beliefs to produce a posterior distribution of potential point values. Probabilities are interpreted as subjective degrees of belief.

For a crude example, say we flip a coin many times. In frequentist statistics we say that the probability of heads is the fraction of heads over the number of flips, so if P(heads) = 0.5 then over many coin flips about half of the flips should come out heads.

In Bayesian statistics we have a prior belief about the fairness of the coin, expressed as a distribution. A normal distribution centered at 0.5 means “I believe the coin is fair, but I wouldn’t be so surprised if it was a tiny bit biased towards heads or tails. As the bias increases, so does my surprise.”

By contrast, a uniform prior would indicate “I have no idea whether the coin is biased, I would believe all biases equally.” A uniform prior makes Bayesian statistics behave like frequentist statistics: our result will be based solely on the coin flips we observe.

As we flip the coin we gather evidence, and update our posterior distribution, indicating our current belief about the coin’s nature. The posterior distribution functions much like the prior distribution: “based on our priors and gathered evidence, we would be most confident that the coin’s bias is 0.49, but 0.48 and 0.50 wouldn’t be so surprising, and 0.8 would be much more surprising.”

Given enough evidence, Bayesian and frequentist statistics will converge to the same answer. If we flip the coin a million times and it clearly turns heads 80% of the time then any Bayesian will yield, “my priors were wrong, the evidence is overwhelming.” However, given limited evidence and an accurate prior, Bayesian techniques can converge more quickly. The Bayesian style of thinking is well-suited to network inference tasks, where we have a model, some prior beliefs about the parameters of that model, and gathered evidence about a network.

Bayes’ Theorem

A foundation of Bayesian statistics is Bayes’ theorem (Bae’s theorem if you really love Bayesian stats) which allows us to take a formula for the probability of observations given a model configuration, and invert it to obtain the probability of a model configuration given our observations. The theorem is as follows:

Or, in Bayesian language:

I find this equation impenetrably dense without an example. Say we’re in a windowless room and a student walks in with wet hair, and I want to know whether it’s raining. I can say:

That is, the probability that it’s raining given that someone walked in with wet hair is based on:

1. The probability that they’d have wet hair if it were raining. Are they carrying an umbrella?
2. The probability that it’s raining. If we are in a desert then there are likely better explanations.
3. The probability that the student’s hair is wet. If their hair is always wet (maybe they take a shower right before office hours) then this is not a useful signal.

Bayesian Statistics in Network Science

We use Bayesian statistics in two ways during network analysis:

1. Predicting model parameters given a network generated by the model
2. Predicting edges based on observations, given an underlying model

Estimating p from a G(n,p) graph

Say we have an adjacency matrix A. That is, a 2D matrix of zeros and ones such that A[i,j] indicates whether there is an edge from node i to j (if A[i,j]=1), or not (A[i,j]=0). This is an undirected graph, so A[i,j]=A[j,i]. We think this matrix was generated by an Erdős-Rényi random graph: that is, every possible edge exists with a uniform probability p. We want to estimate that p value. We’ll start with the opposite problem: given an ER graph parameterized by p, what is the probability of generating adjacency matrix A?

How many edges should we expect in an ER graph with n nodes and p edge probability? Well, we know there are N(N-1)/2 possible edges (every node can connect to every node except itself, divide by 2 because a->b and b->a represent the same edge), or N choose 2, and each occurs with probability p, so for m edges we can expect m = p * (N choose 2). But let’s work from the opposite direction. If each edge exists with probability p, then the probability of generating a given graph is:

That is, every edge that exists in the graph should exist with probability p, and every edge that does not exist in the graph will be absent with probability 1 - p. We can rewrite the expression more concisely:

For convenience, let’s reparameterize in terms of the size of the graph with m edges and n vertices:

That is, the likelihood of generating a graph is given by the probability of an edge for each edge that exists (m), times the probability of no edge for each edge does not exist (n choose 2 possible edges, minus the m edges that actually exist).

Now, given a graph A, what is the most likely p? We want argmax p of l(p), or the p that maximizes the likelihood of the graph. How do we solve for this? With partial derivatives and maximum likelihood estimation (MLE). Specifically, we want to set the partial derivative of l(p) with respect to p to zero:

When the derivative is zero we have an inflection point, typically a local maxima, minima, or saddle point. However, because the likelihood is a concave function we know there will only be one inflection point at the global maxima.

Useful fact: The argmax of l(p) will also be the argmax of log l(p). Why useful? Because in logs products become sums, which are much easier to differentiate. Additionally, our probabilities will often be very tiny, which presents numeric instability with floating point numbers. Logarithms will boost our probabilities into a higher range and stabilize calculations.

This matches our intuition: the edge probability is equal to the graph density, which is the percentage of possible edges that actually exist. Success!

Toy Example

I’ve prepared two networks which you can find here. We want to know whether they are random graphs or not. To determine this, let’s fit a G(n,p) random graph model to each dataset.

#!/usr/bin/env python3
import networkx as nx
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import math

def estimateP(G):
    edges = G.number_of_edges()
    return edges / math.comb(G.number_of_nodes(), 2)

G1 = nx.read_adjlist("data/mystery_adj_list1.txt")
G2 = nx.read_adjlist("data/mystery_adj_list2.txt")

p1 = estimateP(G1)
p2 = estimateP(G2)

Now we will produce a hundred random graphs with those parameters, measure some attributes of those networks, and compare our two real networks to the reference distributions. If our real graphs are random, they should fall comfortably within the bell curve of similar networks. If they are not random, some attributes may fall well outside the reference distributions.

def generateNetworks(n, p, c):
    networks = []
    for i in range(c):
        G = nx.gnp_random_graph(n,p)
        networks.append(G)
    return networks

ref1 = generateNetworks(G1.number_of_nodes(), p1, 100)
ref2 = generateNetworks(G2.number_of_nodes(), p2, 100)

rows = []
for G in ref1:
    t = nx.transitivity(G)
    a = nx.average_shortest_path_length(G)
    d = nx.degree_assortativity_coefficient(G)
    rows.append((t,a,d,"1"))
for G in ref2:
    t = nx.transitivity(G)
    a = nx.average_shortest_path_length(G)
    d = nx.degree_assortativity_coefficient(G)
    rows.append((t,a,d,"2"))
df = pd.DataFrame(rows, columns=["Transitivity", "Avg. Shortest Path Length", "Assortativity", "Distribution"])

df2 = df.melt(id_vars=["Distribution"], var_name="Metric")
g = sns.FacetGrid(df2, col="Metric", row="Distribution", sharex=False, sharey=False, despine=False, margin_titles=True)
g.map(sns.kdeplot, "value")
g.axes[0,0].axvline(x=nx.transitivity(G1), color='r')
g.axes[0,1].axvline(x=nx.average_shortest_path_length(G1), color='r')
g.axes[0,2].axvline(x=nx.degree_assortativity_coefficient(G1), color='r')
g.axes[1,0].axvline(x=nx.transitivity(G2), color='r')
g.axes[1,1].axvline(x=nx.average_shortest_path_length(G2), color='r')
g.axes[1,2].axvline(x=nx.degree_assortativity_coefficient(G2), color='r')
plt.show()

As we can see, the top row, representing the first network and reference distributions, looks plausibly random. The graph’s transitivity, average shortest path length, and degree assortativity are all well-within range for ER networks with the same number of nodes and edges. By contrast, the bottom row is clearly not random: the degree assortativity is similar to that of a random network, but transitivity and shortest path length are definitively not. In fact, the second network comes from the Watts-Strogatz small-world model. Similar number of nodes and edges, similar degree sequence, very different structure.

A visual comparison of the networks would also make the difference clear, but we’re working with statistics today, not guessing at network models from images:

These tools are sufficient to take a mathematical model for network generation, calibrate it to real-world data to find the parameters most likely to yield the observed network, and then used the tuned model to determine whether the network was plausibly generated by such a model. This can help us categorize networks and definitely say “this network is not random,” “this network may have a powerlaw degree sequence, but has structure that is decidedly not explained by the preferential attachment of the Barabasi-Albert model,” and so on.

In the next post, we will explore inferring what edges in a network might exist by applying statistical analysis to observations of interactions.

Section 230: A Primer

Posted 12/13/2025

Senator Whitehouse (D, RI) announced that he’s moving to file a bill to repeal Section 230, the singly most important piece of Internet legislation, which goes on the chopping block a few times a year. While Section 230 is flawed, repealing it without any transition plan in place would be a civil rights disaster. Many have written articles about it. This one is mine.

Who is responsible for the Internet?

The core question is who is legally liable for content posted online, and what responsibility do social media platforms carry for the content they distribute? We have two analogies to draw from:

1. A newspaper. When a newspaper publishes an article, they bear legal responsibility for distributing its contents, and can be sued for libel. Even if the article is written by someone outside the paper, the newspaper editor chose to print the article and so accepts some responsibility for its dissemination.

2. A community tack board at your local coffee shop. Anyone can walk in and tack up whatever they want on the board. The coffee shop owner does not immediately bear liability for what members of the public have put up on the wall, and shouldn’t be sued because a patron tacked up a hateful or libelous message.

So which category does the Internet fall into? When someone posts a video or comment on YouTube, Instagram, Facebook, and so on, does the platform bear responsibility for distributing that content to others?

Before 1996 the legal standard used to rest on whether the platform exerted editorial control. If the platform had content moderation, then they chose what to remove from their platform, and implicitly what to leave up. If the platform had no moderation whatsoever then they could claim similar immunity to a coffee shop as passive facilitators. This meant that Internet service providers were legally in the clear - they fall in the same category as phone companies or the postal service in that they facilitate your communication without being a publisher - while forums and chat rooms were treated more like newspapers. As the Internet grew, this position became untenable: a human moderator can’t approve every Tweet and YouTube video before they go live, and these services can’t exist if social media companies accept legal liability for what every user posts online.

Enter Section 230 of the Communications Decency Act of 1996, which clarifies:

No provider or user of an interactive computer service shall be treated as the publisher or speaker of any information provided by another information content provider.

In short, platforms aren’t responsible for what their users post. There’s a short list of exceptions - platforms are required to take down material violating federal criminal law, copyright restrictions, or human trafficking law. Online services that exist to facilitate illegal transactions are also still vulnerable, so an online drug market can’t claim that they’re not responsible for all their users buying and selling drugs. But in general, this law allows social media to exist, allows any user-submitted online content to exist, and allows platforms to enact content moderation without automatically claiming legal liability for everything they host.

What’s wrong with 230?

A common critique of Section 230 is that it goes too far: platforms bear very little responsibility for the content they host, even if that content is hateful or harmful. For example, it is exceedingly difficult to sue Roblox for endangering children, even though it’s well documented that predators use their game platform to groom and harm children, because they aren’t responsible for what their players post. It is likewise very difficult to hold Meta accountable even when their own research showed that their platforms were dangerous for young people.

While Section 230 means that platforms can moderate content as they see fit, it also means that they don’t have to. The only real incentive platforms have to moderate content at all are market incentives: if a social media platform becomes a vile cesspool of hate and harassment, users may eventually flee to greener pastures that promise to keep out the Nazis. Unfortunately, switching costs are high: if I leave Twitter, I lose all my Twitter follows and followers. Even if those users have also migrated to Mastodon or Bluesky, there is not an easy way to re-establish those relationships en masse. So things have to get pretty bad for a critical mass of users to leave a platform, meaning in practice there is little pressure for the big players to moderate anything at all.

As we face more misinformation, more hate and harassment, and more AI slop online, it’s understandable that people cry out for the government to do something to pressure companies and improve our online spaces.

Why do we still need 230?

Unfortunately, simply repealing Section 230 would immediately destroy the Internet as we know it. Social media platforms like Reddit, Facebook, TikTok, YouTube, and Twitch could not exist. Collaborative writing projects like Wikipedia could not exist. Services like reviews on Google Maps or Yelp or Amazon could not exist, nor could Patreon or Kickstarter - any service where users contribute content could only continue to operate if a company moderator first examined the content to be sure the company wouldn’t be taking on unacceptable legal risk by distributing it. A blog like mine could survive because I don’t have a commenting system at time of writing, but that’s as close as we’d have to the Internet we know.

Technically, these platforms could continue to operate without any moderation, arguing that they’re just a passive conduit for users rather than publishers. However, given the sheer number of spam bots online, removing all moderation would also doom online platforms to collapse.

Why does this keep happening?

Every time there’s a new story about teen self-harm, or mass shooters radicalized online, or a range of other atrocities, politicians are pressured to hold social media accountable. Republicans in particular would like to target social media platforms for “censoring right-wing voices,” a largely baseless conspiracy that is impossible to pursue because companies are free to moderate content as they see fit. While social media companies usually push back against attempts to repeal 230, some larger companies see an advantage in “pulling up the ladder;” operating an army of content moderators would be exceedingly expensive for Facebook, but impossible for its smaller competitors, solidifying a permanent monopoly.

Is there any alternative?

Not an easy one. We don’t want to hold platforms legally liable for everything that users post, whether through exposing them to lawsuits or through some draconian government censorship board. For all the many flaws of social media, it is also an outlet for political and cultural expression, a platform for organizing and spreading information outside of traditional corporate media publishing, and a means of finding and building community with others. Those are ideals worth fostering.

In my opinion, one of the best courses of action is to build online platforms that are not profit-driven. A profit incentive implies keeping moderation costs down, and keeping engagement up to drive advertising revenue. This can lead (often unintentionally!) to dark patterns like encouraging radicalization and ‘hate-scrolling,’ because seeing more extreme and angry content keeps people watching. These incentives encourage lax moderation that won’t drive away users and inhibit ad money. By contrast, a community self-run platform like Mastodon has no advertising, no recommendation algorithm, and no incentive structure except wanting to provide a community space. Self-organized social media brings a host of other challenges related to content moderation and sustainable finances, but these seem to me to be more approachable than curtailing the behavior of Meta or Elon Musk through changing federal law.

RPI’s Vaccine-Autism Study

Posted 9/23/2025

The Centers for Disease Control and Prevention intend to award a no-bid contract to Rensselaer Polytechnic Institute to study whether childhood vaccination induces autism. I studied at RPI through my bachelors and masters degrees, and like many alumni, I am incensed. On September 15th I wrote the following letter in protest:

Dear Dr. Schmidt, Board of Trustees, and Deans,

I am a proud alumnus of Rensselaer (B.S. 2018, M.S. 2020), and credit the institute with shaping me as a professional scientist. I write today with grave concern about Rensselaer’s proposed contract with the CDC to study links between vaccinations and autism ¹.

Rensselaer’s commitment to knowledge and thoroughness is well-known. However, the link between vaccines and autism, first proposed in a now-retracted 1998 paper ², has been conclusively investigated and discredited ^{3 4 5}. Scientific consensus is clear, and further studies are not warranted. Instead of providing certainty, Dr. Juergen Hahn’s proposed work will provide legitimacy to vaccine skeptics by suggesting that a causal link between vaccination and autism is even conceivable.

Vaccine hesitancy is on the rise globally, in part driven by perceived risk of vaccination ⁶. In contributing to this hesitancy, Rensselaer will be complicit in decreasing vaccination rates, a return of once-defeated diseases like measles, and ultimately, unnecessary suffering and early deaths. I urge the institute to reconsider their CDC contract, for the good of humanity and their own reputation.

Respectfully,
Dr. Milo Z. Trujillo

My letter was quoted by the local paper, and other alumni have sent their own letters, started a phone calling campaign, and circulated a petition. I am not optimistic that our efforts will sway RPI’s administration against the value of their CDC contract, but I believe it is imperative to try. After President Trump’s press release asserting autism is caused by Tylenol and vaccines, we’re likely to see greater drops in childhood vaccination. Scientists that entertain the thoroughly dismissed vaccine-autism link are fueling the flames and legitimizing Trump’s claims, and children will suffer and die as a result.

Word Prominence: A Primer

Posted 6/9/2025

A common task in natural language processing is determining what a text (a book, speech, tweet, email) is about. At its simplest, we may start by asking what words appear most prominently in a text, in the hope that they’ll be topic key-words. Here “prominence” is when a word appears disproportionately in this text compared to others. For example, “the,” “a,” and “and” will always appear with high frequency, but they appear with high frequency in every text and are uninteresting to us.

Our approach will start by reducing a text to a list of words and a count of how many times they occur, typically referred to as a bag of words model. This destroys sentence structure and context, a little like burning an essay and sifting through the ashes, but hey, it keeps the math simple, and you have to start somewhere.

For all of the techniques outlined below we’ll need two texts: the text we’re interested in studying, and a “baseline” corpus of text for comparison.

TF-IDF

Our first contender for identifying keywords is term-frequency inverse-document-frequency or TF-IDF. For each word in our text of interest we’ll first measure the frequency with which it occurs, or literally the number of times the word appears divided by the total number of words in the text. For example in Python, if t is a particular term and d is a dictionary of words and how many times they appear, then:

def tf(t, d):
    total = sum(d.values())
    return d[t] / total

Then we’ll examine a number of other texts for comparison, and count how many of those texts contain the target word. Formally the inverse document frequency is defined as:

Or in Python, if D is a list of documents (where each document is a dictionary of terms and how many times they appear, as in tf):

def idf(t, D):
    total = 0
    for d in D:
        if( t in d.keys() ):
            total += 1
    return math.log(len(D) / total)

This means if a term appears in all N documents we’ll get idf(t, D) = log(N/N) = 0, and the fewer documents a term appears in, the higher its IDF score will be.

We can combine term-frequency and inverse-document frequency as simply term-frequency times inverse document frequency, or:

Now terms that appear in many documents will get a low score, and terms that appear in the target document with low frequency will get a low score, but terms that appear with relatively high frequency in the text of interest and appear in few other documents will get a high score.

What does this get us in practice? Well, to borrow Wikipedia’s example, we can compare every play by Shakespeare (I grabbed the Comedy, History, and Tragedy selection from here). Here are the top terms in Romeo and Juliet, sorted by their TF-IDF scores:

The top terms in the play by term frequency are “and,” “the,” and “I,” which each appear about 2% of the time - but these terms all have IDF scores of zero because they appear in every play, and so receive a TF-IDF score of zero as well.

However, only one play includes “Romeo.” This makes up almost 1% of Romeo and Juliet - very common, the twelfth most common or so word - but top of the list by TF-IDF standards.

TF-IDF isn’t perfect - it’s identified many of the names of characters, but also words like “Thursday” and “Paris” (not the setting, which is Verona, Italy) that aren’t especially central to the plot. Nevertheless, TF-IDF is impressively effective given its simplicity. So where does it really fall flat?

The biggest shortcoming of IDF is that it’s boolean: a term either appears in a document or not. However, in large corpora of text we often require more nuance than this. Consider trying to identify what topics a subreddit discusses by comparing comments in the subreddit to comments in other subreddits. In 2020 people in practically every subreddit were discussing COVID-19 - it impacted music festivals, the availability of car parts, the cancellation of sports games, and had some repercussion in almost every aspect of life. In this setting Covid would have an IDF score of near zero, but we may still want to identify subreddits that talk about Covid disproportionately to other communities.

Jensen-Shannon Divergence

Jensen-Shannon Divergence, or JSD, compares term frequencies across text corpora directly rather than with an intermediate “does this word appear in a document or not” step. At first this appears trivial: just try tf(t, d1) - tf(t, d2) or maybe tf(t, d1) / tf(t, d2) to measure how much a term’s frequency has changed between documents 1 and 2.

The difference between term frequencies is called a proportion shift, and is sometimes used. Unfortunately, it has a tendency to highlight uninteresting words. For example, if “the” occurs 2% of the time in one text and 1.5% of the time in another text, that’s a shift of 0.5%, more than Capulet’s 0.45%.

The second approach, a ratio of term frequencies, is more appealing. A relative change in frequencies may help bury uninteresting “stop words” like “the,” “a,” and “it,” and emphasize more significant shifts. However, there’s one immediate limitation: if a term isn’t defined in d2 then we’ll get a division-by-zero error. Some frequency comparisons simply skip over words that aren’t defined in both corpora, but these may be the exact topic words that we’re interested in. Other frequency comparisons fudge the numbers a little, adding 1 to the number of occurrences of every word to ensure every term is defined in both texts, but this leads to less mathematical precision, especially when the texts are small.

Jensen-Shannon Divergence instead compares the frequency of words in one text corpus against the frequency of words in a mixture corpus M:

Here, M is defined as the average frequency with which a term appears in the two texts, or M=1/2 * (P+Q). This guarantees that every term from texts P and Q will appear in M. Additionally, D refers to the Kullback-Leibler Divergence, which is defined as:

The ratio of frequencies gives us a measure of how much the term prominence has shifted, and multiplying by P(x) normalizes our results. In other words, if the word “splendiforous” appears once in one book and not at all in another then that might be a large frequency shift, but P(x) is vanishingly small and so we likely don’t care.

Note that JSD is defined in terms of the total amount that two texts diverge from one another. In this case we’re interested in identifying the most divergent terms between two texts rather than the total divergence, so we can simply rank terms by P(x) * log(P(x)/M(x)). Returning to our Romeo and Juliet example, such a ranking comparing the play to Othello (made by the Shifterator package) might look like:

Jensen-Shannon Divergence can find prominent terms that TF-IDF misses, and doesn’t have any awkward corners with terms that only appear in one text. However, it does have some limitations:

• First, JSD is sensitive to text size imbalance: the longer a text is, the smaller a percentage each word in the text is likely to appear with, so measuring change in word prominence between a small and large text will indicate that all the words in the short text have higher prominence. To some extent this problem is fundamental - you can’t meaningfully compare word prominence between a haiku and a thousand-page book - but some metrics are more sensitive to size imbalances than others.

• Second, KLD has a built-in assumption: frequency shifts for common words are more important than frequency shifts for uncommon words. For example, if a word leaps in frequency from 0.00005 to 0.00010 then its prominence has doubled, but it remains an obscure word in both texts. Multiplying the ratio of frequencies by P(x) ensures that only words that appear an appreciable amount will have high divergence. What’s missing is a tuning parameter: how much should we prefer shifts in common terms to shifts in uncommon terms? Should there be a linear relationship between frequency and how much we value a frequency shift, or should it be an exponential relationship?

These two shortcomings led to the development of the last metric I’ll discuss today.

Rank-Turbulence Divergence

Rank-Turbulence Divergence is a comparatively new metric by friends at the Vermont Complex Systems Institute. Rather than comparing term frequency it compares term rank. That is, if a term moves from the first most prominent (rank 1) to the fourth (rank 4) that’s a rank shift of three. In text, term frequency tends to follow a Zipf distribution such that the rank 2 term appears half as often as the rank 1 term, and the rank 3 term a third as much as rank 1, and so on. Therefore, we can measure the rank as a proxy for examining term frequency. This is convenient, because rank does not suffer from the “frequency of individual terms decreases the longer the text is” challenge that JSD faces.

Critically, we do need to discount changes in high rank (low frequency) terms. If a term moves from 2nd most prominent to 12th most prominent, that’s a big change. If a term moves from 1508th most prominent to 1591st, that’s a little less interesting. However, instead of multiplying by the term frequency as in KLD, Rank Turbulence Divergence offers an explicit tuning parameter for setting how much more important changes in low rank terms are than high rank.

For words that appear in one text but not another, rank turbulence divergence assigns them the highest rank in the text. For example, if text 1 contains 200 words, but not “blueberry,” then blueberry will have rank 201, as will every other word not contained in the text. This is principled, because we aren’t assigning a numeric value to how often the term appears, only truthfully reporting that words like “blueberry” appear less than every other term in the text.

The math at first looks a little intimidating:

Even worse, that “normalization factor” is quite involved on its own:

However, the heart of the metric is in the absolute value summation:

If all we want to do is identify the most divergent terms in each text, and not measure the overall divergence of the two systems, then this snippet is enough. It also builds our intuition for the metric: all we’re really doing is measuring a change in inverse rank, with a knob to tune how much we emphasize changes for common words. The knob ranges from 0 (high and low ranked terms are equally “important”) to infinity (massively emphasize shifts in common words, ignoring shifts in rare words). Here’s an example plotting the difference in words used on two subreddits, r/NoNewNormal (which was a covid conspiracy group) and r/CovIdiots (which called out people acting foolishly during the pandemic):

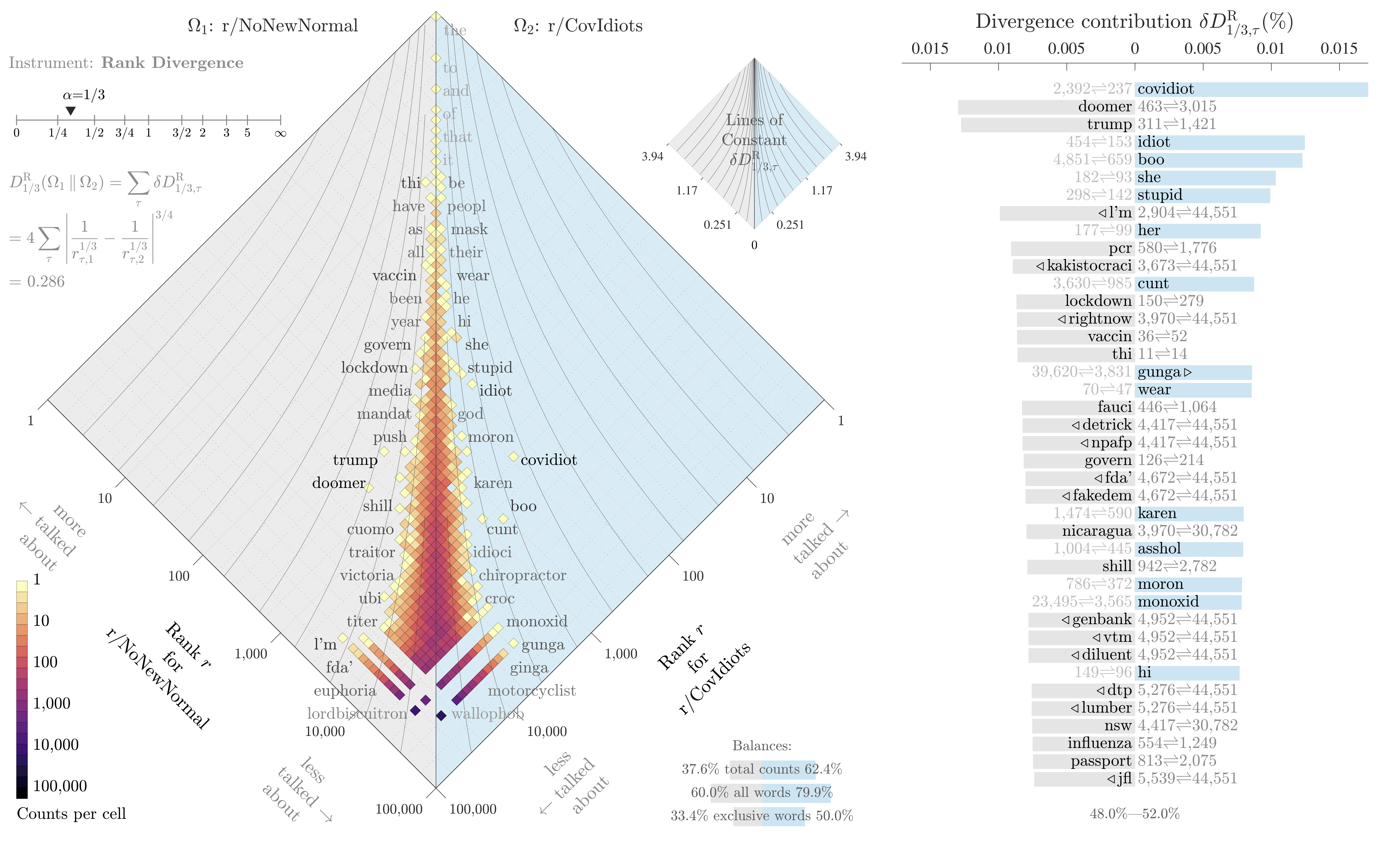
The “divergence contribution” plot on the right can be read like Shifterator’s JSD plot, and simply lists the most divergent terms and which text they appear more in. The allotaxonometry plot on the left reads like a scatterplot, where one axis is the rank of words in r/NoNewNormal and the other axis is the rank of words in r/CovIdiots. When words have the same rank in both texts they’ll appear on the center line, and the more they skew towards one subreddit or another the further out they’ll be plotted. Only a small subset of notable words are explicitly labeled, and the rest of the plot operates more like a heatmap to give a sense of how divergent the two texts are and whether that divergence starts with common words or only after the first thousand or so.

The plot highlights r/NoNewNormal’s focus on lockdowns, doomerism, and political figures like Trump and Fauci, while CovIdiots has a lot more insulting language. The plot correctly buries shared terms like “the” and common focuses like “covid”. That plot comes from one of my research papers, which I discuss in more detail here.

Conclusions

This about runs the gamut from relatively simple but clumsier metrics (tf-idf, proportion shifts) to highly configurable and more involved tools (RTD). The appropriate tool depends on the data - are there enough documents with enough distinct words that tf-idf easily finds a pattern? Splendid, no need to break out a more sophisticated tool. Communicating with an audience that’s less mathy? Maybe a proportion shift will be easier to explain. You have lots of noisy data and aren’t finding a clear signal? Time to move to JSD and RTD.

All of these tools only concern individual word counts. When identifying patterns in text we are often interested in word associations, or clustering many similar words together into topic categories. Tools for these tasks, like Latent Dirichlet allocation and topic modeling with Stochastic Block Models, are out of scope for this post. Word embeddings, and ultimately transformer models from Bert to ChatGPT, are extremely out of scope. Maybe next time.