Infection and Quarantine

Posted 10/23/18

Network Science is a relatively young discipline, which uses a small number of basic models to represent a wide variety of network phenomenon, ranging from human social interactions, to food webs, to the structure of the power grid.

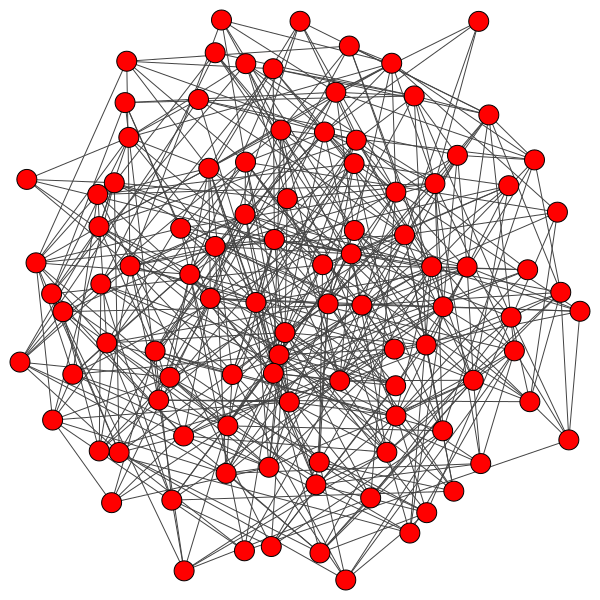
This post focuses on social communities, historically modeled as random networks, where every person has a percent change of having a social connection to any other person. The following is an example of a random network, where the circular nodes represent people, and the edges between circles indicate a social link:

The Topic

Of particular interest to me are information cascades, where some “state” is passed along from node to node, rippling through the network. These “states” can represent the spread of disease, a meme, a political ideology, or any number of things that can be passed on through human interaction.

A starting point for understanding information cascades is disease propagation. Traditionally, infection models run in discrete timesteps, and assume that the infection has a percent chance of spreading across an edge each turn, and will continue to spread until the infected are no longer contagious. This is an adequate model for large-scale disease propagation, where each disease has a different contagious period and infection rate. This basic model is less accurate when applied to small communities, where the differences between individuals cannot be statistically ignored, or when applied to the spread of information rather than disease.

Extensions

Two research papers by Santa Fe Institute researchers extend the infection model to better reflect human behavior and repurpose it to examine the spread of ideas. Duncan Watts’ “A Simple Model of Global Cascades on Random Networks” proposes that each individual has a different susceptibility to infection, which they call an “Activation Threshold”, represented as a percentage of a node’s peers that must be infected before the node will be infected.

To understand this idea, consider a social platform like Twitter or Google+ in its infancy. Some people are early adopters - as soon as they hear a friend is on the platform they will join the platform to participate. Other people are more apprehensive, but once a majority of their peers have Facebook accounts then they, too, will make Facebook accounts so they do not miss out on significant social community. Early adopters have a low activation threshold, apprehensive people have a high threshold.

The result is that a cascade can only succeed in overwhelming a community if it reaches a “critical mass” where adoption is high enough to pass every member’s activation threshold:

If the activation threshold is too high, or the cascade starts in a poor location where many peers have high thresholds, then the cascade will be unable to reach a critical mass, then the infection will fizzle out. This may explain why some ideas, like Twitter or Facebook, succeed, while others like Google+ or Voat, do not. A failed cascade can convert a small cluster of users, but is ultimately contained by high threshold peers:

Akbarpour and Jackson propose a radically different, if simple, extension in “Diffusion in Networks and the Virtue of Burstiness”. They argue that it is insufficient for two people to have a social link for an idea to spread - the users must meet in the same place at the same time. People fall in one of three patterns:

Active for long periods, inactive for long periods. Think of office workers that are only at work from 9 to 5. If two offices are geographically separated, they can only share information while their work days overlap.
Active then inactive in quick succession. Perhaps someone that takes frequent breaks from work to have side conversations with their neighbors.
Random activity patterns. Likely better for representing online communities where someone can check in from their phone at any time.

My Work

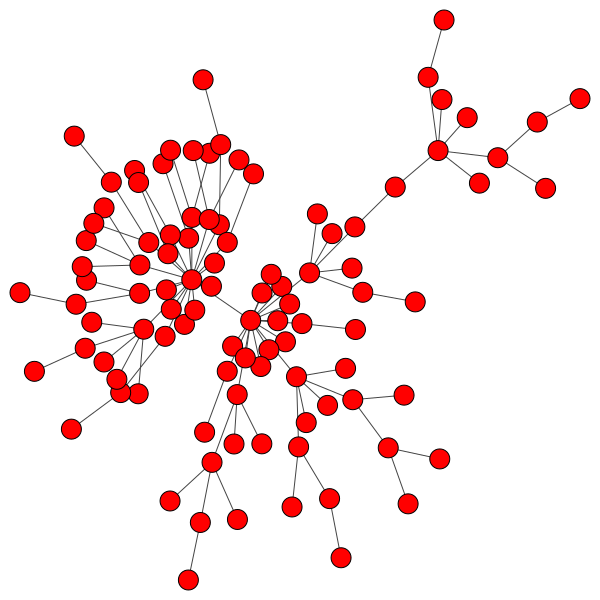
While random networks are simple, human communities are rarely random. Since their introduction in 1999, human communities have more frequently been modeled as scale-free networks. In a scale-free network, new members of the community prefer to connect to well-connected or “popular” members. This results in a small number of highly connected, very social individuals referred to as “hubs”, each with many peers with far fewer connections. Here is an example scale-free network demonstrating the hub-clustering phenomenon:

My objective is to combine the above two papers, and apply the results to scale-free networks. In this configuration, the activity pattern and activation threshold of the hubs is of paramount importance, since the hubs act as gatekeepers between different sections of the network.

When a hub is infected, the cascade will spread rapidly. The hub is connected to a large number of peers, and makes up a significant percentage of the neighbors for each of those peers, since most nodes in the network only have a handful of connections. This means an infected hub can overcome even a relatively high activation threshold.

Compromising even a single hub will allow the cascade to reach new branches of the network and dramatically furthers infection:

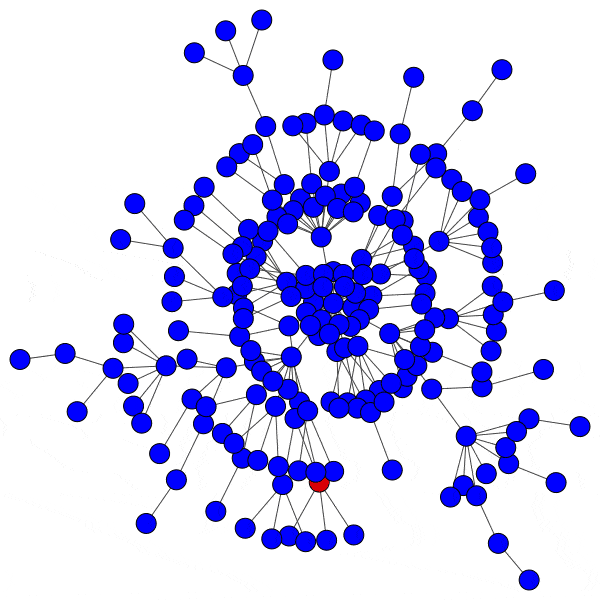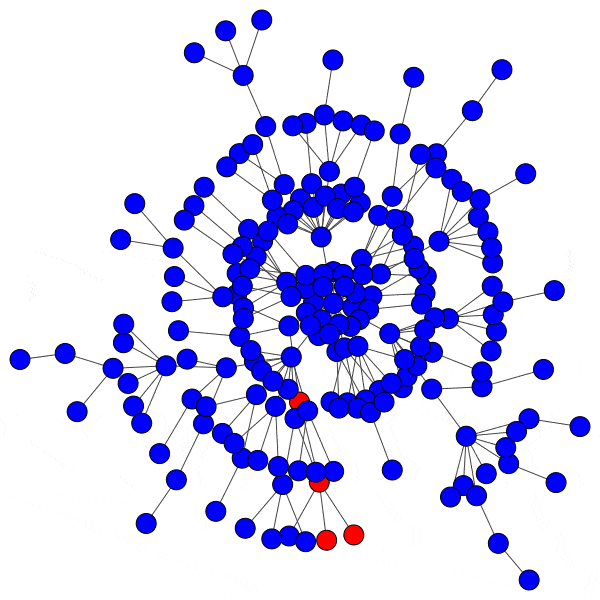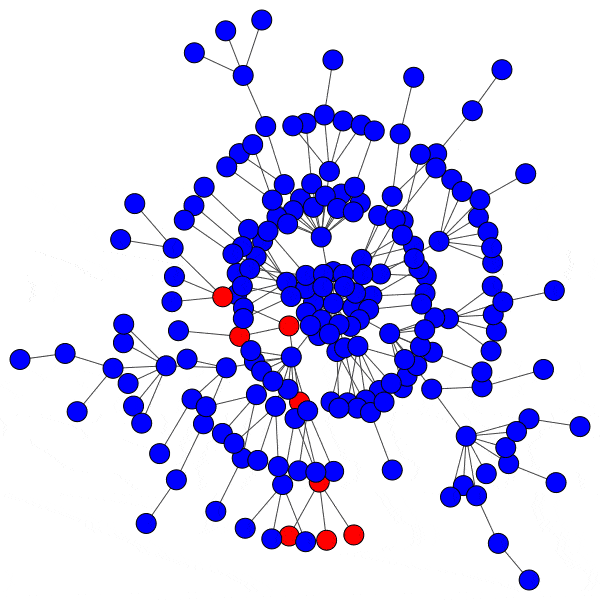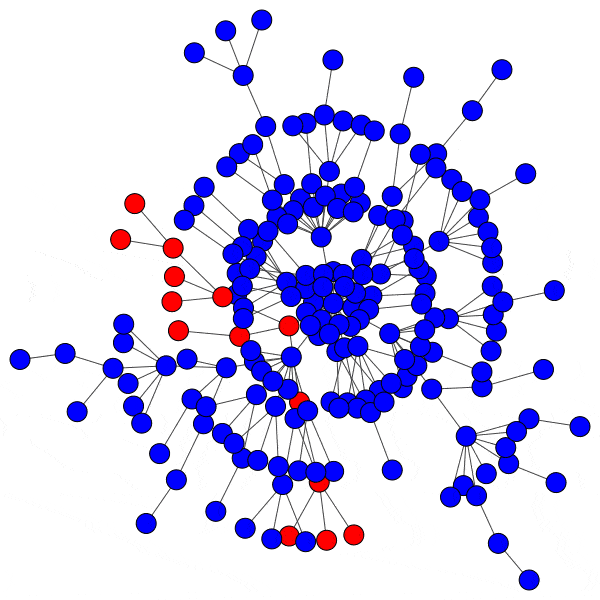
However, infecting a hub is challenging, because hubs have so many peers that even a low activation threshold can prove to be an obstacle. Without capturing a hub, the spread of a cascade is severely hindered:

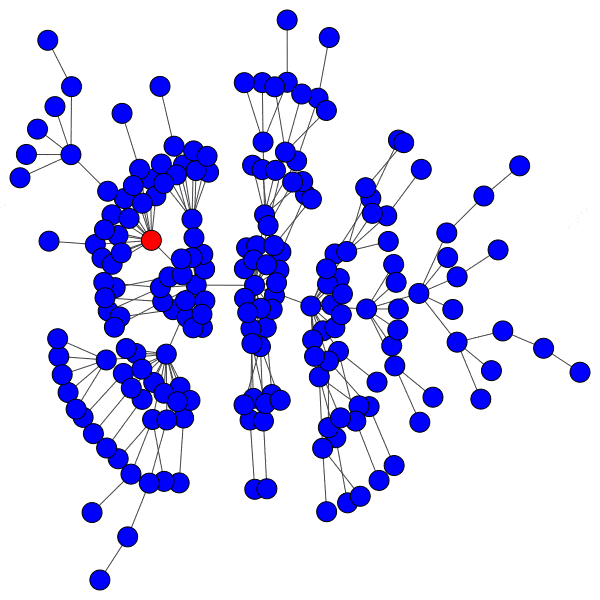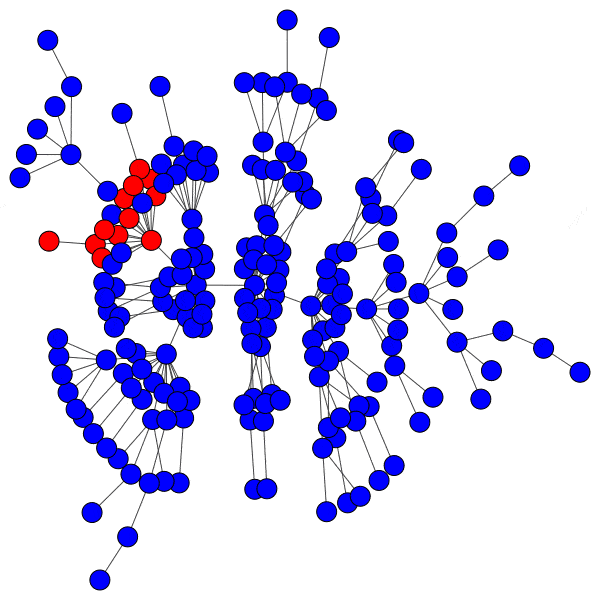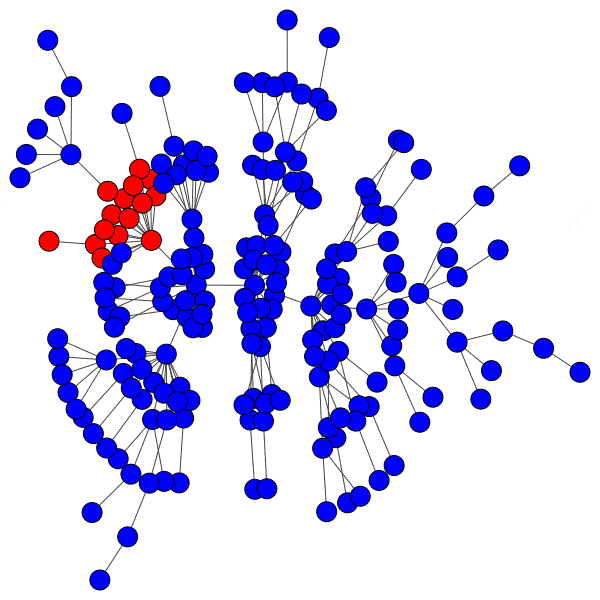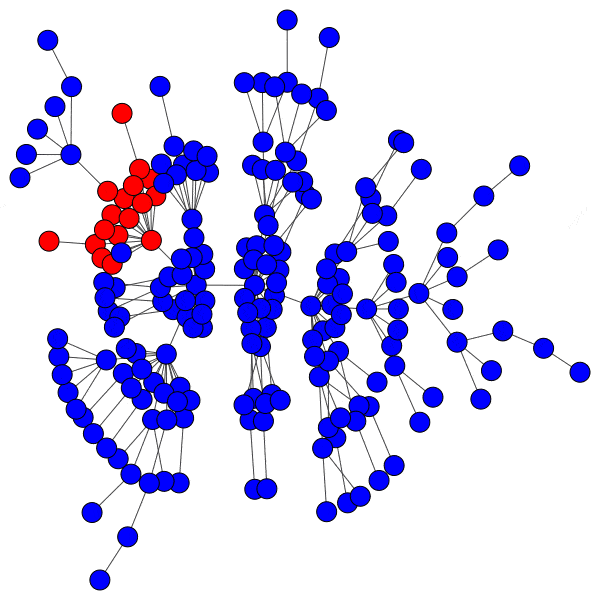
Even with highly susceptible peers, well-protected hubs can isolate a cascade to a district with ease:

Next Steps

So far, I have implemented Watts’ idea of “activation thresholds” on scale-free networks, and have implemented-but-not-thoroughly-explored the activity models from the Burstiness paper. The next step is to examine the interplay between activity types and activation thresholds.

These preliminary results suggest that highly centralized, regimented networks are better able to suppress cascades, but when a cascade does spread, it will be rapid, dramatic, and destabilizing. A fully decentralized, random network has far more frequent and chaotic cascades. Is there a mid-level topology, where small cascades are allowed to occur frequently, but the thread of a catastrophic cascade is minimized? I would like to investigate this further.