
Steganography and Steganalysis with Fourier Transforms
Posted 5/8/19
This post is a high-level introduction to hiding messages in images using Fourier Transforms on the color data. This technique is less susceptible to accidental destruction than techniques like Least Significant Bit steganography, while remaining far more challenging to detect than metadata-based approaches like storing secret messages in image comments. No background in steganography or Fourier Transforms is expected. This post is largely based on “Image Steganography and Steganalysis”, by Mayra Bachrach and Frank Shih.
Image Steganography, the Basics
Our objective is to hide secret messages, whether they be text or arbitrary files, inside images. Images are an attractive secret-message envelope, since they can be transferred in a number of ways (texting, emails, posting on forums, sharing through Google Photos, etc), and do not raise suspicions in many contexts. Before discussing Fourier Transform steganography, we’ll talk about some simpler approaches as context.
Most images include metadata for storing various statistics about the image contents. This metadata can be viewed and edited with tools like exiftool:
% exiftool qr.png
ExifTool Version Number : 11.01
File Name : qr.png
Directory : .
File Size : 9.7 kB
File Modification Date/Time : 2019:04:27 20:10:55-04:00
File Access Date/Time : 2019:04:27 20:10:57-04:00
File Inode Change Date/Time : 2019:04:27 20:10:56-04:00
File Permissions : rw-rw-rw-
File Type : PNG
File Type Extension : png
MIME Type : image/png
Image Width : 246
Image Height : 246
Bit Depth : 8
Color Type : RGB with Alpha
Compression : Deflate/Inflate
Filter : Adaptive
Interlace : Noninterlaced
Image Size : 246x246
Megapixels : 0.061
A first trivial attempt at message hiding is simply putting your secret message in one of these metadata fields. Unfortunately, this is easy to detect with automated tools, as most images won’t have many human-readable strings in them. This data may also be accidentally deleted, as many web services strip image data intentionally, or unintentionally lose it when translating from one image format (like PNG) to another (like JPG).
A slightly more sophisticated solution is Least Significant Bit steganography. The synopsis is:
-
Every pixel’s color is represented as three bytes, for Red, Green, and Blue
-
A change to the least significant bit will result in a nearly-identical color, and the difference will not be perceptible to the human eye
-
We can represent our secret message as a binary sequence
-
We can set the least significant bit of each pixel to the bits from our secret message
Done! And no longer trivially detectable! Even if someone does find your message, it will be hard to prove it is a secret message if it’s encrypted. Unfortunately this method is also susceptible to accidental breaks: If an image is resized or translated to another format then it will be recompressed, and these least significant bits are likely to be damaged in the process.
We want an equally secret message encoding system that is as difficult to detect, but less susceptible to damage.
Fourier Transforms
The math behind Fourier Transforms is complicated, but the intuition is not. Consider a sine wave:
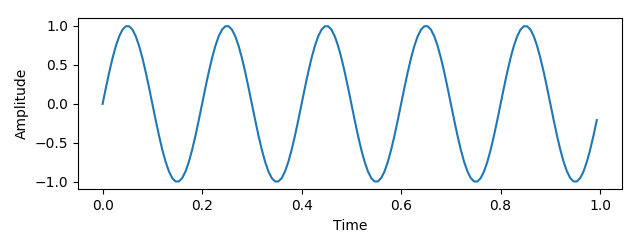
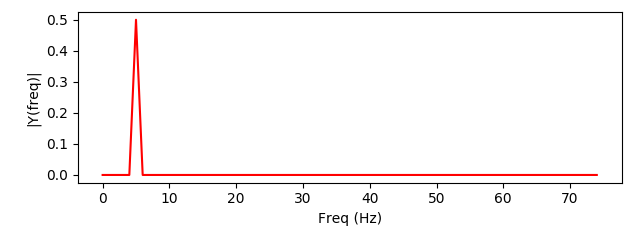
This wave can be described as a frequency and amplitude - let those be x- and y-coordinates in 2-D space:
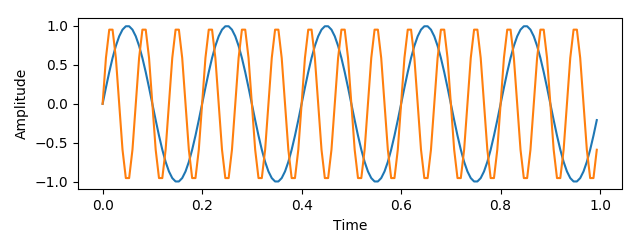
We can add a second wave, with a different frequency:
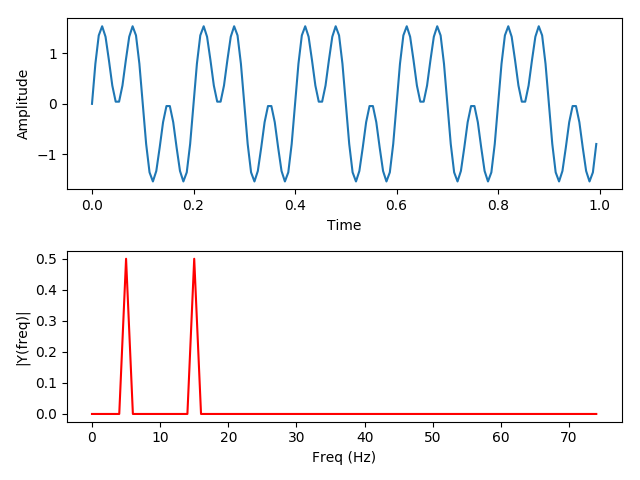
And when we combine the two signals we can represent the combination as two points in frequency-amplitude space, representing the two waves we’ve added:
(The code used to generate the above images can be found here)
This leads to three conclusions:
-
Any arbitrarily complicated signal can be represented as a series of sine waves, layered on top of one another
-
A finite-length signal can be represented with a finite number of sine waves
-
The original signal can be reconstructed by taking the constituent sine waves and combining them
The Discrete Fourier Transform is an algorithm that derives these waves, given a signal of finite length described as discrete samples.
Why would we want to represent waves in this way? A plethora of reasons. Noise reduction, by deleting all waves with an amplitude below a specific threshold. Noise isolation, by deleting all waves not within a specific frequency range (such as the human vocal range). Noise correction, by shifting the frequency of some waves (as used in auto-tune). Ultimately, the Fourier Transform is the foundation of much audio, video, and image compression and manipulation.
Converting Images to a Fourier Matrix
The paper is a little hand-wavey on this part, but images can be expressed as a layering of sine and cosine waves with input based on the pixel coordinates. As with the one-dimensional Fourier transforms used in audio analysis, this process can be reversed to reproduce the original image. The number of samples and waves used determines the accuracy of the approximation, and thus the accuracy when inverting the function to recreate the original image. This video goes into further detail on the process, which is commonly used for image editing and compression.
Embedding and Extracting Messages using Fourier Series
Next, the user expresses their embedded message as a Fourier series. This can be done in a variety of ways, from adapting the waveform of an audio message, to encoding text as a bitsequence and solving the Fourier series for that sequence, to simply Fourier encoding a second image. Once the user has a message encoded as a Fourier series they can easily superimpose the signal by adding coefficients to the corresponding polynomials in the image matrix. The matrix can then be reversed, translating from the frequency domain back to the spatial image domain. The effect is a slight dithering, or static, applied to the image. By shifting the frequency of the hidden message up or down the user may adjust the static properties until a subtle effect is achieved.
The steganographic data can be relatively easily extracted given a copy of the original image. Comparing the pixels of the original and modified image can demonstrate that something has been changed, but not a discernible pattern that can be distinguished from artifacting resulting from lossy image compression, such as what one would see by switching the data format from PNG to JPEG. However, by converting both images to their Fourier matrix representation and subtracting from each other, anyone can retrieve the polynomial representing the encoded message. If the message was frequency adjusted to minimize visual presence, it must now be frequency shifted back, before decoding from Fourier to the original format (audio, bitsequence, etc).
If the unaltered image is not available, because the photo is an original rather than something taken from the web, then a simple delta is impossible. Instead, statistical analysis is necessary. Once again, the Fourier transform is critical, as it allows for pattern recognition and signal detection, differentiating between normal image frequencies and the structured data resulting from layering a message on top of the image.
Steganalysis with Fourier Transforms
The same Fourier-delta technique can be used for the more difficult task of detecting and extracting steganography of an unknown format. In this case, we are given an image, and need to establish both whether there is a hidden message, and preferably, what it is. Given an arbitrary image, we first need to establish a baseline. We can perform a reverse image search and find similar images, with an identical appearance but different hashes. We then compare each baseline image to the possibly steganographic image by converting both to Fourier matrices and calculating a delta, as above. We must then perform noise reduction to remove minor perturbations such as image re-encoding and re-sizing artifacting. If the remaining delta is statistically significant, then there is evidence of a secret signal. This completes the first step, identifying the presence of a steganographic message.
Unfortunately, interpreting this identified message is beyond the scope of the paper. Both participants in a secret conversation can pre-agree on an encoding scheme such as audio, bitstrings, or an embedded image. Given only a frequency spectrum, an analyst needs to attempt multiple encodings until something meaningful is produced. Particularly if the frequency-shifting outlined above has been performed, this is an extremely tedious process, better suited (at least so far) to manual inspection and intuitive analysis than a purely automated design.